Exploring the accuracy of the truncated wavelet transform

import numpy as np

import jax

import matplotlib.pyplot as plt
from matplotlib import gridspec
import matplotlib.patches as patches

import WDM

Time series properties.

dt, N, Nt, Nf = 0.5, 512, 64, 8

assert Nf*Nt==N, "Incompatible dimensions"

Generate a white noise time series signal with r.m.s. value of 1.

key = jax.random.key(0)
key, subkey = jax.random.split(key)
x = jax.random.normal(subkey, shape=(N,)) # white noise

Perform a bunch of different wavelet transforms with different truncation \(q\) parameters. We quantify the accuracy of the transformation by performing a forward (truncated) and inverse (exact) wavelet transformation and looking at the largest absolute difference between the original and recovered time series.

Allowed values of \(q\). Must be an integer in the range \(1\leq q \leq N_t/2\equiv 32\).

q_vals = [1,2,4,8,10,12,14,16,20,25,32]

err_vals = np.zeros(len(q_vals))

for i, q in enumerate(q_vals):
    wdm = WDM.WDM.WDM_transform(dt=0.5,
                                Nf=Nf,
                                N=N,
                                q=q,
                                calc_m0=True)

    w = wdm.forward_transform_truncated(x)

    x_recovered = wdm.inverse_transform(w)

    err_vals[i] = np.max(np.abs(x - x_recovered))

We will also compare this with the error when using the exact forward transform. The exact transform should be same as the truncated transform when \(q=N_t/2=32\).

wdm = WDM.WDM.WDM_transform(dt=0.5,
                            Nf=Nf,
                            N=N,
                            calc_m0=True)

w = wdm.forward_transform_exact(x)

x_recovered = wdm.inverse_transform_exact(w)

err = np.max(np.abs(x - x_recovered))

Plot the errors in the truncated wavelet transform as a function of the truncation parameter.

fig, ax = plt.subplots()
fig.suptitle("Truncated Wavelet Transform Error")

ax.plot(q_vals, err_vals, marker='o', label='Truncated')
ax.axhline(err, color='k', lw=3, linestyle=':', label='Exact')

ax.set_xlabel(r"$q$")
ax.set_ylabel(r"Max error")

ax.set_yscale('log')

ax.grid()
ax.legend(loc='upper right')

plt.show()

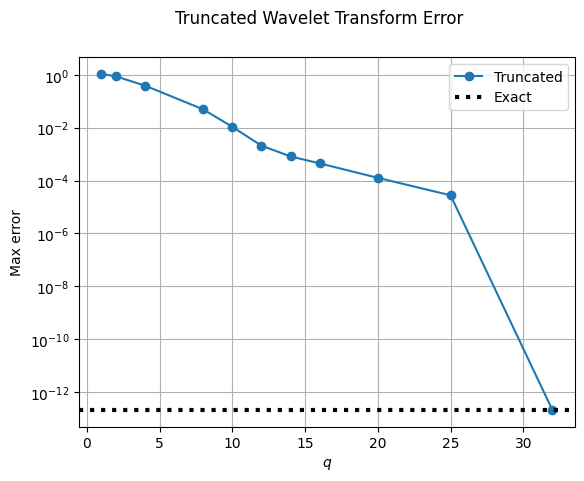
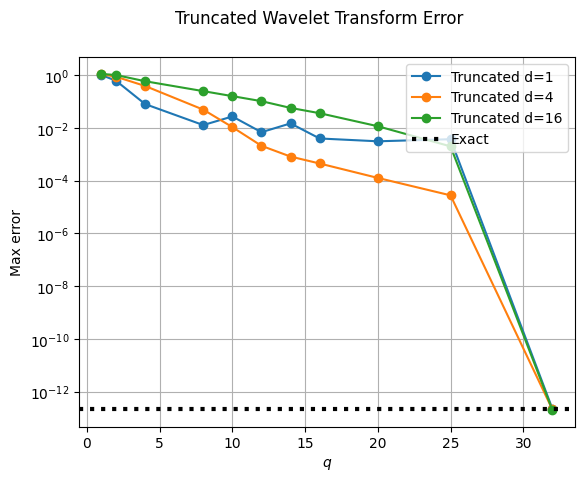
The accuracy of the truncated wavelet transformation also depends on the value of \(d\). Wavelets with smaller d are slightly better localised in time leading to a slightly more accurate truncated transformations for small \(q\).

d_vals = [1, 4, 16]

q_vals = [1,2,4,8,10,12,14,16,20,25,32]

err_vals = {}

for j, d in enumerate(d_vals):

    err_vals[d] = np.zeros(len(q_vals))

    for i, q in enumerate(q_vals):
        wdm = WDM.code.discrete_wavelet_transform.WDM.WDM_transform(dt=0.5,
                                                                    Nf=Nf,
                                                                    N=N,
                                                                    q=q,
                                                                    d=d,
                                                                    calc_m0=True)

        w = wdm.forward_transform_truncated(x)

        x_recovered = wdm.inverse_transform(w)

        err_vals[d][i] = np.max(np.abs(x - x_recovered))

fig, ax = plt.subplots()
fig.suptitle("Truncated Wavelet Transform Error")

for d in d_vals:
    ax.plot(q_vals, err_vals[d], marker='o', label=f'Truncated {d=}')
ax.axhline(err, color='k', lw=3, linestyle=':', label='Exact')

ax.set_xlabel(r"$q$")
ax.set_ylabel(r"Max error")

ax.set_yscale('log')

ax.grid()
ax.legend(loc='upper right')

plt.show()